Writing a research paper means communicating your idea to the external world. The task is always demanding, but it gets better with practice. This tutorial is for students writing their first research paper in machine learning. The paper can be either your semester project report or a submission to a conference. The tips below cover both cases, so please take the time to study the tips; revisit those tips while writing the first draft of your paper.
Your goal is handing in a well-thought and well-written paper; reaching that state requires multiple steps. There are a number of incredible tutorials and presentations out there (see the end of the post). The tutorial below is divided into two main parts: i) tips on how to get started and write the first section of the paper, and ii) general tips for refining the paper.
Writing one section (at the time)
Let us start from the first round of writing, i.e., populating the first section of the paper. Importantly, papers are not written in the order they appear in the final paper, so you do not need to start from the introduction. In fact, we rarely start writing from the introduction. Then, assuming we want to start from the experimental section, the following the next steps should already provide a first version of that section:- Include the tables/results even if the final numbers are not yet ready.
- Write 2-3 sentences that provide the results and comments on them, e.g., does the proposed method perform on par with the baselines? What is the strongest empirical evidence? If your results are not conclusive yet, you can postpone this and the next step until a later point.
- Then, write a couple of sentences on why the reader should care for the experiment, and whether the improvement is important, e.g., is it consistent across the experiments?
- Then, start developing further the details of your experiments. What are the datasets you used? Could you describe the datasets briefly? Are those standard benchmarks?
- Next up, you can write a paragraph (or more) about the implementation details. What are the hyper-parameters that require explanation for reproducibility?
- Are there some additional experiments or toy settings that you need to include?
- Collect all the text, put it in a logical order (e.g., implementation details should come before the experimental results), and revise the text to make it more concise.
Each of the steps should be easy to write down, so do not move on to the next one, until you complete the previous step. These seven steps are meant as a guide for writing the first round of the first section of your paper, while similar steps can be considered for other sections as well.
Should the first section be the experimental section? Not necessarily, I suggest you to start from the section you are most comfortable writing about. For instance, you should be able to identify the works most closely related to yours and write the differences in the related work. Similarly, the theorems you have proved are already determined and you could write them down in the methodology.
General tips on writing
You have now finished writing the first round, is this the first draft? Not yet, there are a couple of steps that you should follow to make the manuscript more accessible:- The paper is not a diary to be written in a chronological order. The fact that you conduct an experiment first, does not mean that this experiment should necessarily be included first; especially if you are writing for a conference submission that has a limited number of pages.
- Notation, notation, notation. The notation is a critical component of your paper (especially for theoretical works) and it should be consistent throughout the text. A couple of simple rules are the following:
- Symbols used in equations should be used in math mode in the text, as well. For instance, 'we use symbol K for [vvv]' should be replaced by 'we use symbol $K$ for [vvvv]'.
- Superscripts are often required, and there are several combinations, e.g., K$^{th}$ or $K^{th}$. Please use $K^{\text{th}}$ in every case for superscripts.
- If specific styling is used for symbols, it should be consistent throughout the paper. For instance, if vectors are denoted in bold (btw, the package bm is recommended for those), they should be bold throughout the text.
- Math equations should either finish with a comma (,) or a period (.), depending on whether there is a sentence continuing/explaining after the equation.
- Use distinctive symbols and avoid overloading notation, e.g., do not use both $u$ and $\upsilon$, unless necessary.
- Abbreviations:
- Even though each task has a number of abbreviations, the reader might not be aware of those. Thus, use the full name the first time and define the abbreviation, and then you can refer to the abbreviation in the rest of the paper. For instance, 'Neural networks (NNs)' defines the new abbreviation that can be used then.
- Define an abbreviation only if you need one; for instance, if you do not use the abbreviation in the rest of the text, you do not need to define it.
- Abbreviations (including datasets, methods, model names) should be consistent throughout the text. One way to guarantee that is by using aliases in LaTeX. For instance, you can define '\newcommand{\cifarten}{Cifar-10}' in the preamble and then refer to it as \cifarten throughout the paper. Even simple abbreviations can be written differently in different parts of the text, e.g., Cifar10, CIFAR10, Cifar-10; thus, using abbreviations is recommended for consistency.
- The '\cite{}' commands: Many ML conferences have established the commands of \citet and \citep which can cause confusion. In case those commands exist in your template, here are a couple of tips on using them more effectively:
- \citet can be used when you want to refer to the authors in the flow of the sentence. For instance, 'the method of \citet{authors}' results in the following text: 'The method of Authors et al.'.
- \citep is used when you want to include parentheses. For instance, 'NNs can be used for synthesising images \citep{authors}' results in the following text: 'NNs can be used for synthesising images (Authors et al.)'.
- Replace 'The authors in \citet{authors}' with '\citet{authors}'.
- LaTeX Labels: First-time users of LaTeX often do not use \label{}, but the label command a great tool in LaTeX enabling you to refer to the equation/figure/section at a later point. The labelling rules I am following are the following:
- Devote the first few characters on the type of label. For instance `eq' for equation, `sec' for section, `fig' for figure. This is especially helpful in case you are writing in IDEs with auto-complete.
- The next few characters should describe the role of the equation. Is it the main model equation or just the first model?
- Follow a similar pattern for labelling. My advice is [type-of-label]:[role]_[additional-info]. For instance, \label{eq:model1_recursive} is distinctive enough for the context of the paper.
- In the equations, write the label at the end, just before the \end{equation} command.
- Write a label in every section, every table/figure and every equation.
- Avoid duplicate labels. Frequently, an equation/table is copied and modified to express a new model/experiment, but the labels are not modified accordingly. The duplicate label creates issues due to the LaTeX compilation. Unfortunately, they show up as 'warnings' in popular cloud-based editors, such as Overleaf, so it would be easy to ignore them.
- References: The style of the references is often overlooked, however the following simple rules can vastly improve the style:
- Accepted papers should be cited with the identifier of the conference/journal, rather than the ArXiv version. Attention: Google Scholar often provides the citation for the ArXiv version and not the accepted in the conference/journal.
- The style and the names of conferences/journals should be consistent. An easy way to achieve that is by defining an abbreviation in the bibtex file and then replacing the booktitle with that. For instance, if you define @STRING{ICLR = "International Conference on Learning Representations"}, now you can write the 'booktitle=ICLR' in the respective field of a citation.
- Pay special attention to citing the correct papers for datasets and benchmarks.
- Figures and tables:
- The captions should be self-contained, descriptive and concise. For instance, writing 'Accuracy on CIFAR10' is not enough; a more descriptive caption could be: 'Comparison of the different architectures when trained on CIFAR10. Notice that the $\Pi-$net requires less parameters than ResNet to achieve the same accuracy, which exhibits the expressivity of the proposed model.'
- Styling: If you have multiple figures/tables that depict the same topic, it is recommended to use the same styling (e.g., line shape, line color, legends).
- Make it easy for the reader to understand if higher or lower values are better. This can be achieved by including a dedicated symbol, e.g., $\downarrow$.
- The best value (per metric per experiment) should be converted into a bold value to be easily identifiable.
Acknowledgements
I am thankful to Zhenyu Zhu, Zhiyuan Wu, Bohan Wang, Aleksandr Timofeev for the feedback they provided and tips on the LaTeX basics.
Resources
The list I compiled above covers only the basics, there is a wealth of additional resources that you can easily access and understand further how to write your research paper.
Video tutorials from incredible researchers:
- YouTube tutorial by William Freeman on writing a paper in computer vision/machine learning: https://youtu.be/W1zPtTt43LI?t=543.
- Tutorial from Simon Peyton Jones on writing a paper in computer science: https://www.youtube.com/watch?v=VK51E3gHENc (supporting material here: https://www.microsoft.com/en-us/research/academic-program/write-great-research-paper/).
- YouTube tutorial by Anthony Newman on writing a paper in (life) science(s): https://www.youtube.com/watch?v=oVF4c6JTAHs.
Booklets and other resources on writing:
- Booklet on writing research papers: http://www.raewynconnell.net/p/writing-for-research.html.
- Blogpost on writing books: https://github.com/mnielsen/notes-on-writing/blob/master/notes_on_writing.md.
- Blogpost with advice for authors: https://jsteinhardt.wordpress.com/2017/02/28/advice-for-authors/.
- Book: 'How to write a research paper', by Simon Kendall.
- Session in deep learning indaba: https://pdf4pro.com/view/how-to-write-a-great-research-paper-deeplearningindaba-com-4f629c.html.
Useful resource: 'The elements of style', style guide for writing in English.
TopThe semester project requires few tools that should be mostly familiar to you through your previous project in computing and machine learning (ML). Most of the tutorials below are introductory; they will probably not cover everything you need, but they should provide fundamental tools for your project.
- Git tutorial: Git is a core part of the code you will write. Git enables easy tracking of changes and is a powerful ally for avoiding unwanted changes. The recommended plan is to have a private repository that will be updated on a weekly basis.
- If you haven’t heard of git, there are incredible tutorials on the internet. Please follow this basic tutorial. Please do not skim through it, but rather complete it. You can choose any repository you like for the parts that require a link from a repo. Even better, you can create a private repo that you will use for the project and complete the tutorials based on this private repo.
- After you complete the tutorial please create a private github repository; if you did that in the previous step, that’s awesome.
- Tmux tutorial: Tmux is a very useful tool that you can use in a remote server (if you are connected to one). The idea is that this tmux session in the remote server will remain open even after you close your ssh connection.
- Please go ahead and study the following tutorial. If you have a Windows machine, it might not be convenient to install it, so you can skip the installation.
- Also, if you want to do more splitting of windows or use fancy formatting options, you can find details here. This is optional, since even basic tmux can do the job.
- Debugging python scripts: Mistakes are (almost) unavoidable when writing (python) code, hence one of the crucial components is how to learn to resolve them quickly.
- Even though there is not a unique way to debug, there are a couple of recommended practices that can be useful for faster debugging. This is an absolutely essential tutorial. The command ‘pdb.set_trace()’ can be used when issues with your code are faced.
- Complementary ways to debug can be found, for instance using the logging/printing and the assert as this tutorial stresses out.
- In the beginning you might also simply google your error, it is highly likely that for simple errors the first answer of google will provide a fix. However, the goal is to rely increasingly on your skills and pdb to find and fix the errors fast.
- LaTex tutorial: LaTex is a tool required for the report and the outcomes of this project.
- If you have not used LaTex before, I recommend spending some time getting accustomed to it. Even if you have written in Latex before, please do check out these tutorials.
- There are few cloud-based LaTeX editors; I recommend Overleaf; when you complete the tutorials below, you can open a new project on Overleaf and try the commands they share yourself.
- A basic tutorial for LaTex is this. Please complete it by copying their commands in a new project in overleaf.
- A complimentary tutorial that includes more commands is this.
- PyTorch tutorial: PyTorch is a machine learning framework that you most probably need for the project.
- If you have not used PyTorch before, please go ahead and complete the following basic tutorial.
- If you have used PyTorch before for building your own model, I recommend checking the visualization tools at your disposal in PyTorch, e.g. through Tensorboard or TensorWatch. Most of those visualizations can be achieved outside of Tensorboard/TensorWatch, but those provide an easy interface to inspect the model during training.
- A basic (but useful) cheatsheet for your project is this.
Abstract
We propose a new class of function approximators based on polynomial expansions. The new class of networks, called Π-nets, express the output as a high-degree polynomial expansion of the input elements.
The unknown parameters, which are naturally represented by high-order tensors, are estimated through a collective tensor factorization with factors sharing. Changing the factor sharing we can obtain diverse architectures tailored to a task at hand. To that end, we derive and implement three tensor decompositions.
We conduct the following diverse experiments: we demonstrate results in image (and pointcloud) generation, image (and audio) classification, face recognition and non-euclidean representation learning. Π-nets are very expressive even in the absence of activation functions. When combined with activation functions between the layers, Π-nets outperform the state-of-the-art in the aforementioned experiments.
Architectures of polynomial networks
The idea is to approximate functions using high-degree polynomial expansions. To explain how this would work, let us showcase it with a third-degree polynomial expansion. Then, assuming the input is a d-dimensional vector z, we want to capture up to third-degree correlations of the elements of z. Let xt denote the scalar output of the polynomial expansion and W[k] denote the kth degree parameters. Then, the polynomial expansion would be:
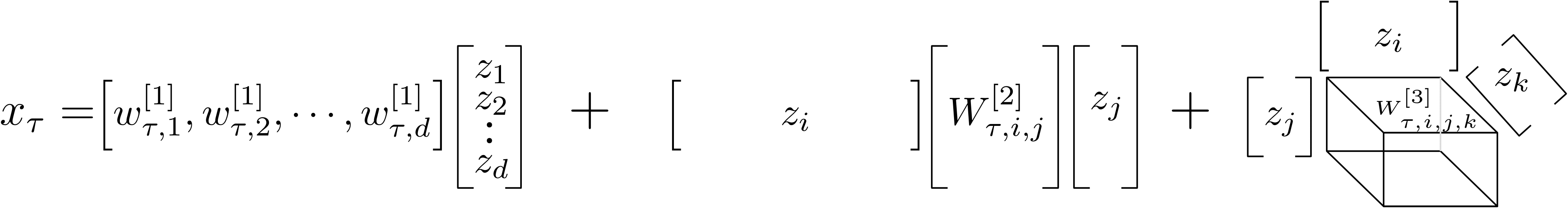
The expression above captures all correlations of element zi with zj, where i, j belong in the [1, d] interval. However, the unknown parameters W[k] scale very fast with respect to the degree of the polynomial. Our goal is to use high-degree expansions on high-dimensional signals, such as images. Therefore, we should reduce the number of unknown parameters.
Tensor decompositions have been effectively used to reduce the number of unknown parameters in the literature. Indeed, we use collective tensor factorization and we can reduce the unknown parameters significantly. In addition, we can obtain simple recursive relationships that enable us to construct arbitrary degree polynomial expansions. The details of the derivations can be found in the papers.
For instance, different architectures that perform polynomial expansions of the input z:
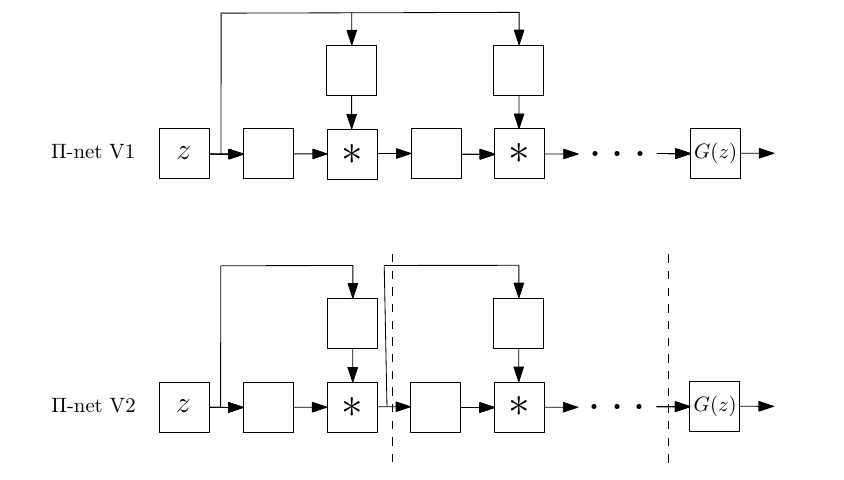
In the paper, we demonstrate results in a number of tasks, outperforming strong baselines. For instace, you can find some images generated by the proposed Π-nets below:

BibTeX
@article{poly2021,
author={Chrysos, Grigorios and Moschoglou, Stylianos and Bouritsas, Giorgos and Deng, Jiankang and Panagakis, Yannis and Zafeiriou, Stefanos},
journal={IEEE Transactions on Pattern Analysis and Machine Intelligence},
title={Deep Polynomial Neural Networks},
year={2021},
pages={1-1},
doi={10.1109/TPAMI.2021.3058891}}
@article{chrysos2019polygan,
title={Polygan: High-order polynomial generators},
author={Chrysos, Grigorios and Moschoglou, Stylianos and Panagakis, Yannis and Zafeiriou, Stefanos},
journal={arXiv preprint arXiv:1908.06571},
year={2019}
}Each clip is cropped from a longer video; each clip consists of 500-4,000 frames. Along with each frame, we provide an (automatically obtained) sparse shape of the face (annotated with the popular 68 markup).
A video with indicative frames from several thousand clips is visualized below:
The dataset is provided strictly for academic use. That is, any type of commercial applications are not allowed; please refer to Youtube license for further details.
To obtain access to the database, please follow the instructions mailed back from our gmail account: 2mf2.db[at].
The dataset is described in details in the following publication: “Motion deblurring of faces”, GG Chrysos, P Favaro, S Zafeiriou, International Journal of Computer Vision https://link.springer.com/article/10.1007/s11263-018-1138-7
]]>VAE are a type of neural network (function approximators) that assume the existence of an undelying low-dimensional space of the data. They try to approximate this latent distribution. You can then sample from this distribution to generate synthetic data. VAE are emerging as a great way to model the latent properties of objects, while one of their interpretations lies in variational Bayesian methods. They remain a hot research topic, so our understanding is not complete.
This review is organised in two parts: in the first part each tutorial is summarised. Then, a table with the attributes of each tutorial are provided. The attributes are organised in three categories: i) background information, ii) main VAE part, iii) applications.
-
fastforward labs: This is a two-part tutorial for VAE; in part 1 VAE are explained as a generalisation of the autoencoder and explain the differences from it. Sequentially, they explain how VAE can be approached from the Bayesian perspective (the author provides a high level intuition). In the second part, they dive more into the practical implementation (python 3, tensorflow). They additionally explain the re-parametrization trick and the final cost function.
-
jmetzen: The author implements VAE step by step in tensorflow and experiments with MNIST. He provides a notebook with the code, very practical for understanding a fundamental implementation.
-
int8.io: The author starts by explaining the benefits of GAN and how it can create artificial samples. However, through the shortcomings of GAN, he introduces VAE as a combination of the Autoencoders and the variational inference. He presents a nice application (face swapping). The focus guides the reader through a practical introduction/understanding to the network’s structure.
-
kvfans: Nice introductory post on explaining VAE. The author provides details on encoding/decoding an image through an example. He introduces VAE as a solution to the shortcomings of GAN.
-
jaan.io: The first part is devoted in an engineering approach of the original paper. The introduction is a bit rough, however the second part is devoted in the theoretical aspect. He derives the lower bound minimisation. As a ‘footnote’, the author provides a splendid explanation of the re-parametrization trick, while the glossary in the end of the article is very handy (it summarises the differences of the neural network vs probabilistic approach). Overall the first part is engineering-based tips, while the second part is more mathematical and demands some math understanding.
-
wiseodd: The author starts with a comparison of GAN vs VAE. Then he retracts and uses a very simple example (imagination process) to provide the intuition of the latent variables. He derives the variational bound (math heavy part); he implements VAE in Keras (python) and explains the re-parametrization trick. Even though the deep learning side is not developed much, personally I find this tutorial quite thorough (from the math side).
-
nutty netter: Short visual introduction in VAE. It starts by explaining why the log likelihood allows the efficient stohastic optimisation, derives the variational bound and then explains VAE as a neural network. The video creator offers some experimental results and some improvements in the original paper. However, he does not explain the reparametrisation trick or the motivation to use VAE instead of the alternatives (mean field, etc).
Following the summation of the articles, the table below describes the core components that are included in each article. The following abbreviations are used:
- ML: machine learning
- AE: autoencoders’ explanation
- LL: log likelihood explanation
- NN: neural network
| Article | Background info | Main part | Applications | Difficulty/Audience |
|---|---|---|---|---|
| fastforward labs | AE,Bayesian learning |
VAE as NN |
- | ML beginners |
| fastforward labs (part2) | - | cost function explanation |
- | requires math understanding |
| jmetzen | - | - | code,results |
engineers |
| int8.io | AE |
VAE as NN |
code,results |
engineers,ML beginners |
| kvfans | - | VAE as NN |
code,results,limitations |
engineers |
| jaan.io | probabilistic/bayesian approach,approximate posterior |
variational bound derivation,re-parametrization trick |
code |
requires math understanding |
| wiseodd | bayesian approach,approximate posterior,intuition |
variational bound derivation,re-parametrization trick |
code |
requires math understanding |
| nutty netter | LL |
variational bound derivation,VAE as NN |
limitations |
requires math understanding |
The tutorials above cover the introduction to VAE from different aspects, however they all have limited explanation on the shortcomings of VAE (e.g. how the Gaussian prior leads to blurry results) or how to adapt VAE to more complex modelling than MNIST. Obviously, these tutorials are introductory in the topic and the actual paper(s) about VAE provide more information on the motivation and derivation of this type of neural network.
]]>In this example, the classifier is trained in the ‘face’ class, i.e. it returns a binary decision whether there is a face in the pixels or not. This post is prepared as part of a seminar of the EESTech Challenge 2016-17 (official site, EESTEC news).
A simple version of this classifier with ~25 lines of code can be built as indicated below, using python and 2 well-tested libraries. In the end of this post, there are some proposals for improving the accuracy of the trained model, extending it for more difficult cases. Aside of the snippets below, the notebook with the complete code can be found here.
If you want to run the code yourself, you should:
- install the menpo library. The recommended way is by installing Anaconda. Among the reasons to install it through anaconda is that a lot of additional package, e.g. scikit learn will be installed along with menpo/menpofit (and you won’t need to spend time with compatible versions, conda will sort it out).
- download the 300W dataset along with the Pascal dataset.
The references are summarised in an increasing length and scientific depth manner, i.e. if you have more time, you can read the ones towards the end. This non-exhaustive list is the following:
- BBC timeline: The development of AI through 15 discrete milestones over the last 70 years. Focus: commercial, political evolution of the subject, it includes links to other BBC articles for each milestone.
- History-extra: The progress in AI divided into 7 eras, starting from ancient Greece. It provides a very brief introduction of the pre-electronic machinery intelligence, while it includes only high level progress of the AI over the last 70 years, mainly through the AI funding decisions.
- History of discriminative learning: A brief introduction to supervised discriminative methods written from an engineering perspective. The author recaps the most popular discriminative techniques, like Support Vector Machines, along with the related scientific articles. It also includes few references to the recent progress in the field of Neural Networks.
- Paper on supervised methods: The history of supervised methods for machine learning. The authors of the paper (Machine learning: a review of classification and combining techniques) provide a more detailed overview of the supervised methods. This article is few years old, so it does not reflect on any recent developments, however it provides a decent introduction to the majority of the methods till then.
- Notes on AI history: The focus is on classic AI techniques, through the performance of AI into games. It includes also a reference to the ALPAC and the Lighthill report that included pessimistic predictions about the (short-term) financial returns and the small-scale success of AI.
- The Quest of Artificial Intelligence: A lengthy book, available from Cambridge University Press, by Nils Nilsson, one of the early contributors of machine learning. The book is quite detailed, it develops the techniques in a chronological order along with several more philosophical questions that led to this development. It also includes (part of ) the motivation for developing the techniques, e.g. how probabilistic reasoning was not included in the early approaches to AI and how the need for probabilistic methods emerged. Definitely recommended if you want a more thorough understanding of the historic portrait of machine learning evolution.
If you happen to know additional links or references, I would be happy to add them to the list.
]]>