Polynomial Nets
Published:
Abstract
We propose a new class of function approximators based on polynomial expansions. The new class of networks, called Π-nets, express the output as a high-degree polynomial expansion of the input elements.
The unknown parameters, which are naturally represented by high-order tensors, are estimated through a collective tensor factorization with factors sharing. Changing the factor sharing we can obtain diverse architectures tailored to a task at hand. To that end, we derive and implement three tensor decompositions.
We conduct the following diverse experiments: we demonstrate results in image (and pointcloud) generation, image (and audio) classification, face recognition and non-euclidean representation learning. Π-nets are very expressive even in the absence of activation functions. When combined with activation functions between the layers, Π-nets outperform the state-of-the-art in the aforementioned experiments.
Architectures of polynomial networks
The idea is to approximate functions using high-degree polynomial expansions. To explain how this would work, let us showcase it with a third-degree polynomial expansion. Then, assuming the input is a d-dimensional vector z, we want to capture up to third-degree correlations of the elements of z. Let xt denote the scalar output of the polynomial expansion and W[k] denote the kth degree parameters. Then, the polynomial expansion would be:
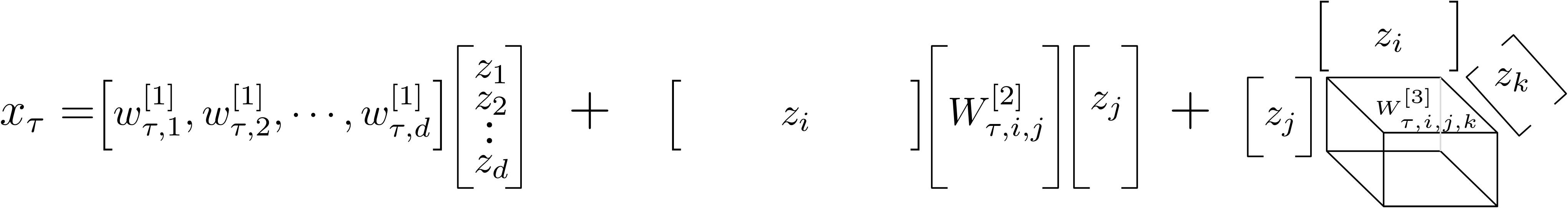
The expression above captures all correlations of element zi with zj, where i, j belong in the [1, d] interval. However, the unknown parameters W[k] scale very fast with respect to the degree of the polynomial. Our goal is to use high-degree expansions on high-dimensional signals, such as images. Therefore, we should reduce the number of unknown parameters.
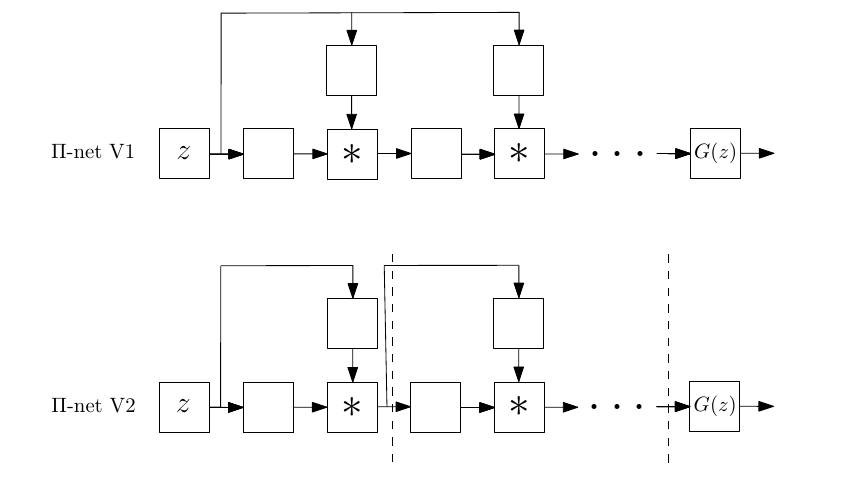
Tensor decompositions have been effectively used to reduce the number of unknown parameters in the literature. Indeed, we use collective tensor factorization and we can reduce the unknown parameters significantly. In addition, we can obtain simple recursive relationships that enable us to construct arbitrary degree polynomial expansions. The details of the derivations can be found in the papers.
For instance, different architectures that perform polynomial expansions of the input z:
In the paper, we demonstrate results in a number of tasks, outperforming strong baselines. For instace, you can find some images generated by the proposed Π-nets below:

BibTeX
@article{poly2021,
author={Chrysos, Grigorios and Moschoglou, Stylianos and Bouritsas, Giorgos and Deng, Jiankang and Panagakis, Yannis and Zafeiriou, Stefanos},
journal={IEEE Transactions on Pattern Analysis and Machine Intelligence},
title={Deep Polynomial Neural Networks},
year={2021},
pages={1-1},
doi={10.1109/TPAMI.2021.3058891}}
@article{chrysos2019polygan,
title={Polygan: High-order polynomial generators},
author={Chrysos, Grigorios and Moschoglou, Stylianos and Panagakis, Yannis and Zafeiriou, Stefanos},
journal={arXiv preprint arXiv:1908.06571},
year={2019}
}